Coefficient of Restitution
An excerpt from the book: "An Introduction to the Physics of Sports" by Dr Vassilios M Spathopoulos.
A basketball bounces more than a tennis ball, the reason being that when colliding with the ground it suffers fewer energy losses. We can determine the percentage of speed that the ball retains after the collision by use of the coefficient of restitution,
 |
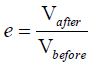Where, Vafter and Vbefore are the speeds before and after the collision.
The larger this parameter is, the more elastic the collision, i.e. the fewer the energy losses. Furthermore, if we let a ball drop from a certain height, the height that it will reach after the rebound is higher for balls with a greater coefficient of restitution. More specifically, it can be proved that the coefficient of restitution is approximately given by,
 |
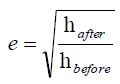Where, hafter and hbefore are the heights after and before the collision.
The symbol √ is that of the square root, which is the number than when multiplied
by itself will give the original number. So for example, the square root of 9 is 3.
For some sports, the heights at which the balls must rebound to are strictly defined.
So in basketball, according to the International Basketball Federation (FIBA), if a ball
is dropped from 1.8m it must return to a height between 1.2m and 1.4m. From the
above formula we can deduce that the coefficient of restitution will lie between,
 |
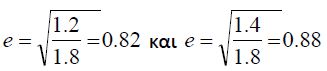In the same way, if a tennis ball is dropped from a height of 100 inches (254cm) on to a concrete floor, it must rebound to a height between 53 inches (134.62cm) and 58 inches (147.32cm). So the limits are,
 |
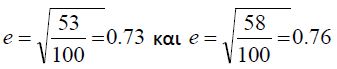A basketball certainly bounces better than a tennis ball.
It is important to note that the coefficient e, depends not only on the type of ball but also on the properties of the ground. This is why the above limits are defined with respect to a concrete floor, as the tennis ball will certainly bounce differently on clay and on grass.
About the Author
Dr Vassilios McInnes Spathopoulos has a PhD in Aerospace and Electronic Engineering from the University of Glasgow (UK). He has also completed a MSc course in Flight Dynamics at Cranfield University (UK). He currently teaches at the Department of Aircraft Technology, at the Technological Education Institute (TEI) of Chalkis, Greece. See more.
Related Pages
- Buy the ebook "An Introduction to the Physics of Sports" by Dr Vassilios M Spathopoulos.
- More articles by Vassilios Spathopoulos
- More on the Physics of Sport
- Other Books on Sports Biomechanics
Any comments, suggestions, or corrections? Please let us know.
Current Events